First propose in , and was later popularized by the Transformer paper, the Attention mechanism has become the backbone of most large language models today.

The goal of the attention mechanism is to compute a context vector for each input element than combines information from all other input elements.

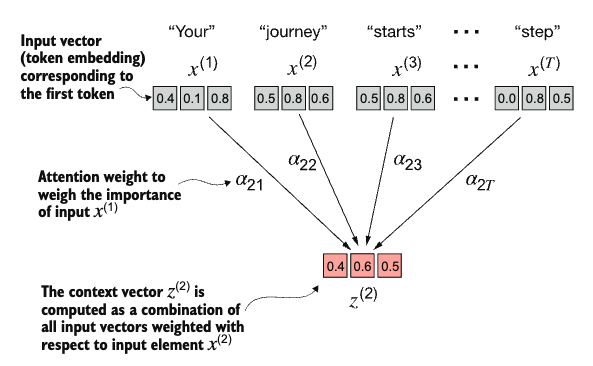
Consider the following input sentence, which has already been embedded into 3-dimensional vectors:

import torch

inputs = torch.tensor(
    [[0.43, 0.15, 0.89],    # Your
    [0.55, 0.87, 0.66],     # journey
    [0.57, 0.85, 0.64],     # starts
    [0.22, 0.58, 0.33],     # with
    [0.77, 0.25, 0.10],     # one
    [0.05, 0.80, 0.55]]     # step
)

Calculating the attention scores

The first step in the attention mechanism is to calculate the intermediate attention scores between the query token and each input token. These scores are computed by taking the dot product of the query (\(x^{(2)}\) in this example), with every other input token in the sentence.

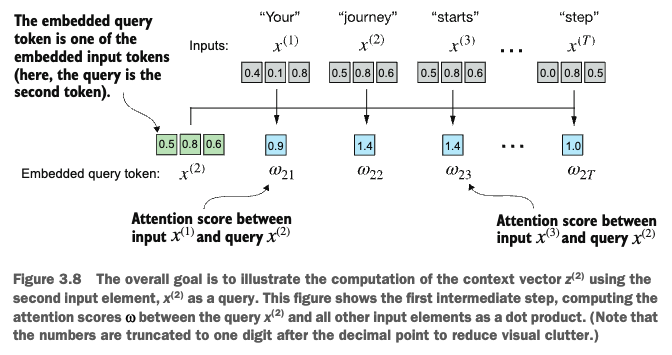
1query = inputs[1]

attn_scores_2 = torch.empty(inputs.shape[0])
for i, x_i in enumerate(inputs):
    attn_scores_2[i] = torch.dot(query, x_i)

print(attn_scores_2)

1: Here, the second input token is being used as the query. Later on we will see that this step is repeated for every input token in the sentence.

tensor([0.9544, 1.4950, 1.4754, 0.8434, 0.7070, 1.0865])

After computing the attention scores, our next step is to normalize it for training stability. The normalized attention scores can also sometimes be referred to as attention weights. One straightforward way of doing so is to divide the scores by the sum of all scores:

attn_weights_2_tmp = attn_scores_2 / attn_scores_2.sum()
print(f"Attention Weights: {attn_weights_2_tmp}")
print(f"Sum: {attn_weights_2_tmp.sum():.2f}")

Attention Weights: tensor([0.1455, 0.2278, 0.2249, 0.1285, 0.1077, 0.1656])
Sum: 1.00

However, this approach can be numerically unstable. A more common approach is to use the softmax function, which exponentiates the scores before normalizing them. The softmax function is defined as follows

\[ \text{softmax}(x_i) = \dfrac{\exp({x_i})}{\sum_j \exp({x_j})}. \]

In code, we could implement it as:

def softmax(x):
    return torch.exp(x) / torch.exp(x).sum()

attn_weights_2 = softmax(attn_scores_2)
print(f"Attention Weights: {attn_weights_2}")
print(f"Sum: {attn_weights_2.sum():.2f}")

Attention Weights: tensor([0.1385, 0.2379, 0.2333, 0.1240, 0.1082, 0.1581])
Sum: 1.00

PyTorch also has a built-in softmax function (which is more numerically stable than our softmax() function) that we can use:

attn_weights_2 = torch.softmax(attn_scores_2, dim=0)
print(f"Attention Weights: {attn_weights_2}")
print(f"Sum: {attn_weights_2.sum():.2f}")

Attention Weights: tensor([0.1385, 0.2379, 0.2333, 0.1240, 0.1082, 0.1581])
Sum: 1.00

We now have the attention weights, we can use them to calculate the context vector \(z^{(2)}\) corresponding to the query token \(x^{(2)}\):

query = inputs[1]
context_vec_2 = torch.zeros(query.shape)

for i, x_i in enumerate(inputs):
    context_vec_2 += attn_weights_2[i] * x_i

print(context_vec_2)

tensor([0.4419, 0.6515, 0.5683])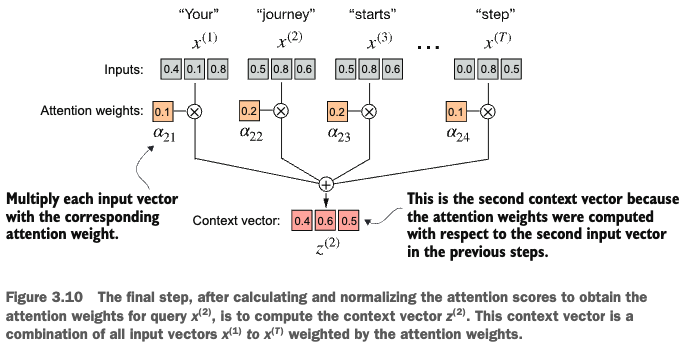

Computing attention weights for all input tokens

attn_scores = torch.empty((inputs.shape[0], inputs.shape[0]))
#print(attn_scores.shape)

attn_scores = torch.matmul(inputs, inputs.T)
1attn_weights = torch.softmax(attn_scores, dim=-1)
all_context_vecs = torch.matmul(attn_weights, inputs)

print(all_context_vecs)

1: By setting dim=-1, we are instructing the softmax function to apply the normalization along the last dimension of the attn_scores tensor. If attn_scores is a two-dimensional tensor (for example, with a shape of [rows, columns]), it will normalize across the columns so that the values in each row (summing over the column dimension) sum up to 1.

tensor([[0.4421, 0.5931, 0.5790],
        [0.4419, 0.6515, 0.5683],
        [0.4431, 0.6496, 0.5671],
        [0.4304, 0.6298, 0.5510],
        [0.4671, 0.5910, 0.5266],
        [0.4177, 0.6503, 0.5645]])

Implementing self-attention with trainable weights

Our next step is the implement the attention mechanism used in the original Transformer architecture, also known as scaled dot-product attention.

Computing the attention weights step-by-step

We will implement the self-attention mechanism by introducing three matrices \(W_Q\), \(W_K\), and \(W_V\) that will be used to project the input tokens into three different spaces: the query space, the key space, and the value space.

x_2 = inputs[1]
d_in = inputs.shape[1] # the input embedding size
d_out = 2  # the output embedding size

In practice, the dimensions of the input embedding and output embedding are often the same. But for illustration purposes, we will set the output embedding size to be 2 for now.

torch.manual_seed(123)

# intialize the weight matrices
W_query = torch.nn.Parameter(torch.randn(d_in, d_out), requires_grad=False)
W_key = torch.nn.Parameter(torch.randn(d_in, d_out), requires_grad=False)
W_value = torch.nn.Parameter(torch.randn(d_in, d_out), requires_grad=False)

# compute the query, key, and value vectors for the second input token
query_2 = x_2 @ W_query
key_2 = x_2 @ W_key
value_2 = x_2 @ W_value

print(f"Query vector: {query_2}")

Query vector: tensor([-1.1729, -0.0048])

Let’s compute the key and value vectors for all input tokens:

keys = inputs @ W_key
values = inputs @ W_value
print(f"Keys shape: {keys.shape}")
print(f"Values shape: {values.shape}")

Keys shape: torch.Size([6, 2])
Values shape: torch.Size([6, 2])

Next, we can compute the attention scores:

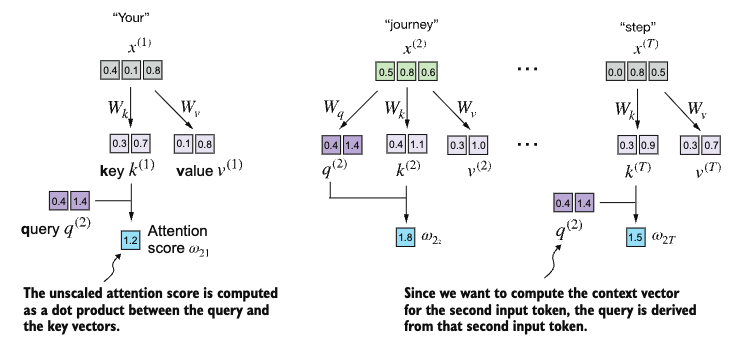
keys_2 = keys[1]
attn_scores_22 = query_2.dot(keys_2)
print(attn_scores_22)

tensor(0.1376)

We can compute the attention scores for all input tokens as follows:

attn_scores_2 = query_2 @ keys.T
print(attn_scores_2)

tensor([ 0.2172,  0.1376,  0.1730, -0.0491,  0.7616, -0.3809])

Let’s now compute the attention weights using the scaled dot-product attention formula:

d_k = keys.shape[-1]
1attn_weights_2 = torch.softmax(attn_scores_2 / (d_k ** 0.5), dim=-1)
print(attn_weights_2)

1: This is the implementation of the legendary formula \(\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\) in the Transformer paper.

tensor([0.1704, 0.1611, 0.1652, 0.1412, 0.2505, 0.1117])

We can now compute the context vector for the second input token:

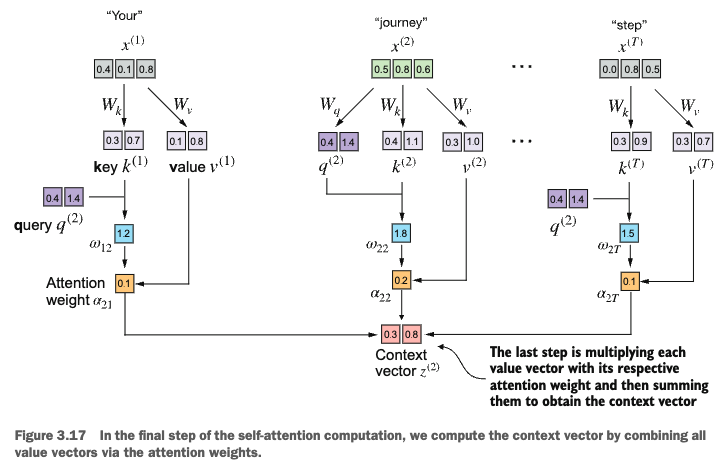
context_vec_2 = attn_weights_2 @ values
print(context_vec_2)

tensor([0.2854, 0.4081])

Implementing a compact self-attention class

import torch.nn as nn

class SelfAttentionv1(nn.Module):
    def __init__(self, d_in, d_out):
        super().__init__()
        self.W_query = nn.Parameter(torch.randn(d_in, d_out))
        self.W_key = nn.Parameter(torch.randn(d_in, d_out))
        self.W_value = nn.Parameter(torch.randn(d_in, d_out))

    def forward(self, x):
        keys = x @ self.W_key
        values = x @ self.W_value
        queries = x @ self.W_query

        attn_scores = queries @ keys.T
        attn_weights = torch.softmax(attn_scores / (keys.shape[-1] ** 0.5), dim=-1)
        context_vecs = attn_weights @ values
        return context_vecs

Let’s do a quick test of our SelfAttentionv1 class for the initial inputs:

sa_v1 = SelfAttentionv1(d_in, d_out)
print(sa_v1(inputs))

tensor([[0.1278, 0.2577],
        [0.1365, 0.2556],
        [0.1364, 0.2556],
        [0.1294, 0.2624],
        [0.1295, 0.2595],
        [0.1310, 0.2618]], grad_fn=<MmBackward0>)

A self-attention class with PyTorch’s Linear layer:

class SelfAttention_v2(nn.Module):
    def __init__(self, d_in, d_out, qkv_bias=False):
        super().__init__()
        self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)

    def forward(self, x):
        keys = self.W_key(x)
        values = self.W_value(x)
        queries = self.W_query(x)

        attn_scores = queries @ keys.T
        attn_weights = torch.softmax(attn_scores / (keys.shape[-1] ** 0.5), dim=-1)
        context_vecs = attn_weights @ values
        return context_vecs

torch.manual_seed(789)
sa_v2 = SelfAttention_v2(d_in, d_out)
print(sa_v2(inputs))

tensor([[-0.0739,  0.0713],
        [-0.0748,  0.0703],
        [-0.0749,  0.0702],
        [-0.0760,  0.0685],
        [-0.0763,  0.0679],
        [-0.0754,  0.0693]], grad_fn=<MmBackward0>)

Masked attention

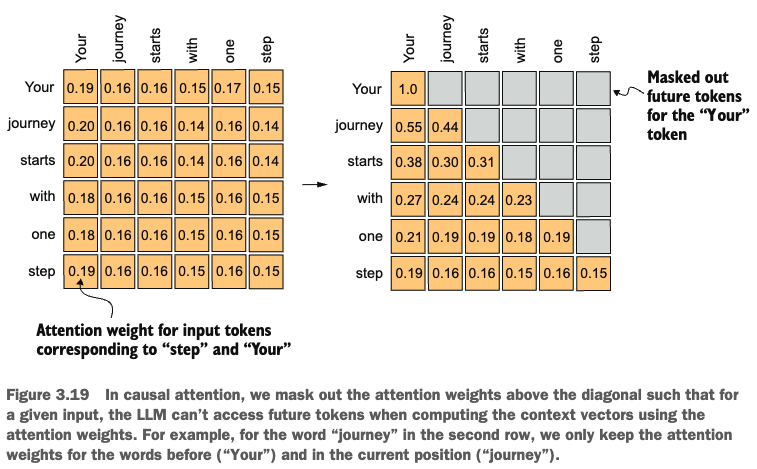
Also known as causal attention, masked attention is a specialized form of self-attention that restricts the model to only consider previous and current inputs in a sequence.

To achieve this, for each token processed, we mask out the future tokens, as illustrated in

queries = sa_v2.W_query(inputs)
keys = sa_v2.W_key(inputs)
values = sa_v2.W_value(inputs)

attn_scores = queries @ keys.T
attn_weights = torch.softmax(attn_scores / (keys.shape[-1] ** 0.5), dim=-1)
print(attn_weights)

tensor([[0.1921, 0.1646, 0.1652, 0.1550, 0.1721, 0.1510],
        [0.2041, 0.1659, 0.1662, 0.1496, 0.1665, 0.1477],
        [0.2036, 0.1659, 0.1662, 0.1498, 0.1664, 0.1480],
        [0.1869, 0.1667, 0.1668, 0.1571, 0.1661, 0.1564],
        [0.1830, 0.1669, 0.1670, 0.1588, 0.1658, 0.1585],
        [0.1935, 0.1663, 0.1666, 0.1542, 0.1666, 0.1529]],
       grad_fn=<SoftmaxBackward0>)

Having obtained the attention weights matrix, we can now create a mask using the tril function in PyTorch:

context_length = attn_scores.shape[0]
mask_simple = torch.tril(torch.ones(context_length, context_length))
print(mask_simple)

tensor([[1., 0., 0., 0., 0., 0.],
        [1., 1., 0., 0., 0., 0.],
        [1., 1., 1., 0., 0., 0.],
        [1., 1., 1., 1., 0., 0.],
        [1., 1., 1., 1., 1., 0.],
        [1., 1., 1., 1., 1., 1.]])

Now let’s apply this mask using matrix multiplication:

masked_simple = attn_weights * mask_simple
print(masked_simple)

tensor([[0.1921, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.2041, 0.1659, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.2036, 0.1659, 0.1662, 0.0000, 0.0000, 0.0000],
        [0.1869, 0.1667, 0.1668, 0.1571, 0.0000, 0.0000],
        [0.1830, 0.1669, 0.1670, 0.1588, 0.1658, 0.0000],
        [0.1935, 0.1663, 0.1666, 0.1542, 0.1666, 0.1529]],
       grad_fn=<MulBackward0>)

and normalize it:

row_sums = masked_simple.sum(dim=-1, keepdim=True)
masked_simple_norm = masked_simple / row_sums
print(masked_simple_norm)

tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.5517, 0.4483, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.3800, 0.3097, 0.3103, 0.0000, 0.0000, 0.0000],
        [0.2758, 0.2460, 0.2462, 0.2319, 0.0000, 0.0000],
        [0.2175, 0.1983, 0.1984, 0.1888, 0.1971, 0.0000],
        [0.1935, 0.1663, 0.1666, 0.1542, 0.1666, 0.1529]],
       grad_fn=<DivBackward0>)

That’s the basic idea to implement masked attention. However, there’s a more efficient way to do it by creating a mask with 1s above the diagonal, then replace these 1s with negative infinity values:

mask = torch.triu(torch.ones(context_length, context_length), diagonal=1)
masked = attn_scores.masked_fill(mask.bool(), -torch.inf)
print(masked)

tensor([[0.2899,   -inf,   -inf,   -inf,   -inf,   -inf],
        [0.4656, 0.1723,   -inf,   -inf,   -inf,   -inf],
        [0.4594, 0.1703, 0.1731,   -inf,   -inf,   -inf],
        [0.2642, 0.1024, 0.1036, 0.0186,   -inf,   -inf],
        [0.2183, 0.0874, 0.0882, 0.0177, 0.0786,   -inf],
        [0.3408, 0.1270, 0.1290, 0.0198, 0.1290, 0.0078]],
       grad_fn=<MaskedFillBackward0>)

Now we just need to apply the softmax function to this maked matrix and then we’re done

attn_weights = torch.softmax(masked / keys.shape[-1]**0.5, dim=1)
print(attn_weights)

tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.5517, 0.4483, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.3800, 0.3097, 0.3103, 0.0000, 0.0000, 0.0000],
        [0.2758, 0.2460, 0.2462, 0.2319, 0.0000, 0.0000],
        [0.2175, 0.1983, 0.1984, 0.1888, 0.1971, 0.0000],
        [0.1935, 0.1663, 0.1666, 0.1542, 0.1666, 0.1529]],
       grad_fn=<SoftmaxBackward0>)

torch.manual_seed(123)

dropout = torch.nn.Dropout(0.5)
print(dropout(attn_weights))

tensor([[2.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.7599, 0.6194, 0.6206, 0.0000, 0.0000, 0.0000],
        [0.0000, 0.4921, 0.4925, 0.0000, 0.0000, 0.0000],
        [0.0000, 0.3966, 0.0000, 0.3775, 0.0000, 0.0000],
        [0.0000, 0.3327, 0.3331, 0.3084, 0.3331, 0.0000]],
       grad_fn=<MulBackward0>)

Implementing a compact causal attention class

batch = torch.stack((inputs, inputs), dim = 0)
print(batch.shape) # two inputs with 6 tokens each, each token has emb_dim = 3

torch.Size([2, 6, 3])

class CausalAttention(nn.Module):
    def __init__(self, d_in, d_out, context_length, dropout, qkv_bias=False):
        super().__init__()
        self.d_out = d_out
        self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_value = nn.Linear(d_in, d_out, bias = qkv_bias)
        self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.dropout = nn.Dropout(dropout)
        self.register_buffer(
            'mask', torch.triu(torch.ones(context_length, context_length), diagonal=1)
1        )
    
    def forward(self, x):
        b, num_tokens, d_in = x.shape

        keys = self.W_key(x)
        values = self.W_value(x)
        queries = self.W_query(x)

        attn_scores = queries @ keys.transpose(1,2) # tranpose to keep the batch at the first dim
        attn_scores.masked_fill_(
            self.mask.bool()[:num_tokens, :num_tokens], -torch.inf)
        attn_weights = torch.softmax(attn_scores / keys.shape[-1]**0.5, dim=-1)
        attn_weights = self.dropout(attn_weights)

        context_vec = attn_weights @ values
        return context_vec

1: automatically move to the appropriate device (CPU or GPU) along with our model

torch.manual_seed(123)
context_length = batch.shape[1]
ca = CausalAttention(d_in, d_out, context_length, 0.0)
context_vecs = ca(batch)
print("context_vecs shape: ", context_vecs.shape)

context_vecs shape:  torch.Size([2, 6, 2])

Extending single-head attention to Multi-head Attention

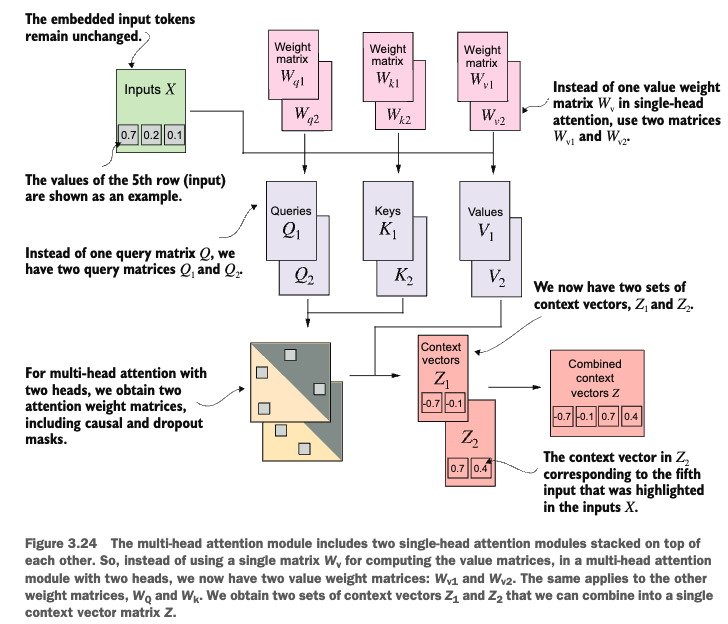
Stacking multiple single-head Attention layers

class MultiHeadAttentionWrapper(nn.Module):
    def __init__(self, d_in, d_out, context_length, dropout, num_heads, qkv_bias=False):
        super().__init__()
        self.heads = nn.ModuleList(
            [CausalAttention(
                d_in, d_out, context_length, dropout, qkv_bias
            )
            for _ in range(num_heads)]
        )
    
    def forward(self, x):
        return torch.cat([head(x) for head in self.heads], dim=-1)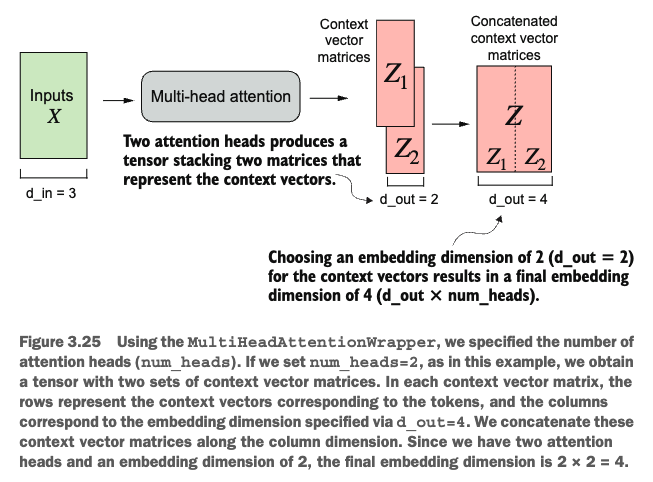

Let’s make things more concrete using a specific example.

torch.manual_seed(123)

context_length = batch.shape[1] # number of tokens
d_in, d_out = 3,2

mha = MultiHeadAttentionWrapper(
    d_in, d_out, context_length, 0.0, num_heads = 2
)
context_vecs = mha(batch)

print(context_vecs)
print("context_vecs.shape:", context_vecs.shape)

tensor([[[-0.5740,  0.2727, -0.3132, -0.2272],
         [-0.7272,  0.1840, -0.2252,  0.0507],
         [-0.7733,  0.1575, -0.2013,  0.1339],
         [-0.7002,  0.1201, -0.1638,  0.1384],
         [-0.6551,  0.1314, -0.1673,  0.1825],
         [-0.6447,  0.1017, -0.1410,  0.1740]],

        [[-0.5740,  0.2727, -0.3132, -0.2272],
         [-0.7272,  0.1840, -0.2252,  0.0507],
         [-0.7733,  0.1575, -0.2013,  0.1339],
         [-0.7002,  0.1201, -0.1638,  0.1384],
         [-0.6551,  0.1314, -0.1673,  0.1825],
         [-0.6447,  0.1017, -0.1410,  0.1740]]], grad_fn=<CatBackward0>)
context_vecs.shape: torch.Size([2, 6, 4])

Implementing Multi-head Attention with weight splits

One problem with the above implementation is that they are processed sequentially [head(x) for head in self.heads]. We can improve this by processing the heads in parallel.

class MultiHeadAttention(nn.Module):
    def __init__(self, d_in, d_out, context_length, dropout, num_heads, qkv_bias=False):
        super().__init__()
        assert (d_out % num_heads == 0), "d_out must be divisible by num_heads"
        self.d_out = d_out
        self.num_heads = num_heads
        self.head_dim = d_out // num_heads
        self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)
        self.out_proj = nn.Linear(d_out, d_out)
        self.dropout = nn.Dropout(dropout)
        self.register_buffer(
            "mask",
            torch.triu(torch.ones(context_length, context_length),
            diagonal=1)
        )

    def forward(self, x):
        b, num_tokens, d_in = x.shape

        keys = self.W_key(x)        # (b, num_tokens, d_out)
        queries = self.W_query(x)   # (b, num_tokens, d_out)
        values = self.W_value(x)  # (b, num_tokens, d_out)

        # split the matrix by adding a num_heads dimension
        # unroll the last dim: (b, num_tokens, d_out) -> (b, num_tokens, num_heads, head_dim)
        keys = keys.view(b, num_tokens, self.num_heads, self.head_dim)
        values = values.view(b, num_tokens, self.num_heads, self.head_dim)
        queries = queries.view(b, num_tokens, self.num_heads, self.head_dim)

        # transpose from (b, num_tokens, num_heads, head_dim) -> (b, num_heads, num_tokens, head_dim)
        keys = keys.transpose(1,2)
        queries = queries.transpose(1,2)
        values = values.tranpose(1,2)

        attn_scores = queries @ keys.transpose(2,3)
        mask_bool = self.mask_bool()[:num_tokens, :num_tokens]

        attn_scores.masked_fill_(mask_bool, -torch.inf)

        attn_weights = torch.softmax((
            attn_scores / keys.shape[-1]**0.5), dim=-1)
    
        attn_weights = self.dropout(attn_weights)
        context_vec = (attn_weights @ values).transpose(1,2) # (b, num_tokens, n_heads, head_dim)
        context_vec = context_vec.contiguous().view(b, num_tokens, -1)
        context_vec = self.out_proj(context_vec)
        return context_vec